Introduction to Regression
Introduction to Regression¶ This tutorial proves an overview of linear regression. It illustrates fitting a polynomial to noisy data, including the role of SSE
April 13, 2022
No Comments
Decision Support Notebooks, Education
Intro to History Matching and Uncertainty Analysis
These videos were prepared as lectures for the Groundwater Modelling topic of the Groundwater Hydrology course at Flinders University. They aim to introduce history matching
October 5, 2021
No Comments
Non-Linear Uncertainty Analysis
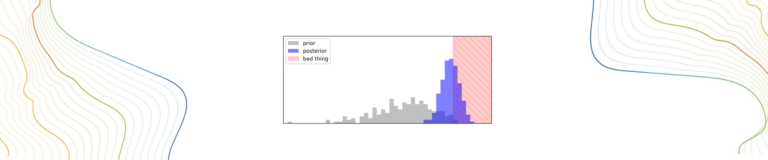
In contrast to linear uncertainty analysis, non-linear methods do not suffer from the limitation of assuming a linear relationship between model predictions and model parameters.
May 31, 2021
1 Comment
Covariance Matrices: The PPCOV Suite
A variance-covariance matrix, often referred to as a covariance matrix, is a square matrix that provides covariances between pairs of elements of a random vector.
May 19, 2021
No Comments
Data Worth Analysis
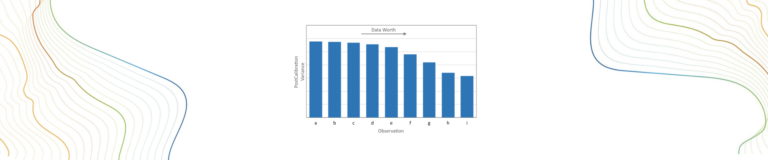
The present tutorial addresses the ability (or otherwise) of yet-ungathered data to reduce the uncertainties of decision-critical predictions using linear analysis utilities from the PEST
May 10, 2021
No Comments
Linear Uncertainty Analysis
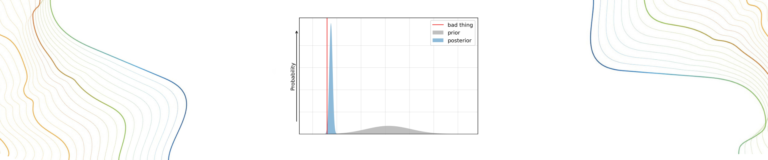
Linear uncertainty analysis is also known as “first order second moment” (or “FOSM”) analysis. It provides approximate mathematical characterisation of prior predictive probability distributions, and
May 3, 2021
3 Comments
Calibration – A Simple Model
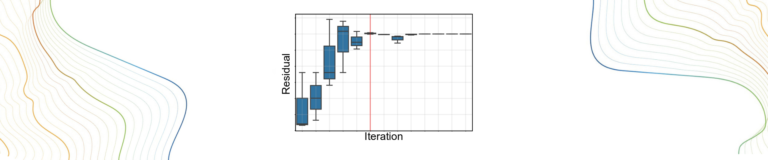
This is the first in a series of tutorials which demonstrate workflows for parameter estimation and uncertainty analysis with the PEST/PEST++ suites. These are not the only
April 19, 2021
3 Comments
How Complex Should a Groundwater Model Be?
https://vimeo.com/566929903 by Catherine More and John Doherty Because environmental systems are complex, models must be complex too. Otherwise, how can they simulate the impact of
April 9, 2021
1 Comment
Uncertainty in Groundwater Modelling 101
https://vimeo.com/548316380 by Catherine Moore and John Doherty We have talked about uncertainty before – in last year’s webinar series. We have been asked to talk
April 9, 2021
1 Comment
OLPROC: Processing Observations Made Easy
OLPROC is a model dancing partner. Its role is to postprocess model outputs in order to match them with field measurements, as well as to
February 23, 2021
No Comments